Neste artigo:
Estacionaridade
Seguros e Derivados
Opções e o caso da Allied Lyons
-----------------------------
Estacionaridade
Vimos no
artigo anterior (http://revolucaoedemocracia.blogspot.pt/2014/01/o-sector-financeiro-vi-jogos-com.html
) que éramos capazes de prever bastante bem a evolução futura da esperança de vida
(EV) baseados em poucos valores do passado, mas o mesmo não se podia dizer
quanto à previsão de futuras taxas de câmbio JPY/USD; ainda que usássemos
informação de outras variáveis económicas (taxas de juro de empréstimo
bancário) a previsão era frequentemente muito má.
A grande
diferença entre as evoluções temporais de EV e de JPY/USD é que, enquanto a
primeira é bastante regular, a segunda é bastante irregular. Procuremos
objectivar o que se entende aqui por «regular», começando por observar abaixo o
gráfico da EV (traço preto).
Claramente a
EV evolui, em termos médios, linearmente. Se subtrairmos à EV uma recta
que «suba» à taxa de 0,137 anos de esperança de vida por ano, obtemos uma recta
horizontal situada no valor de 15,1 anos. (O leitor pode comprovar este e
outros resultados usando os dados de EV do artigo anterior.) Isto é, a menos do
crescimento de 0,137 anos/ano, a média dos valores de EV é constante e igual a
15,1 anos; não varia com o tempo.
Verifica-se
que os desvios face à evolução linear são pequenos e a sua variabilidade
também. Quanto á variabilidade, é usual (por várias razões) medi-la pela raiz
quadrada da média dos quadrados dos desvios; o chamado desvio padrão ([10]). Pois bem, o desvio padrão de
todos os desvios é apenas de 0,2 anos.
Mas não é o desvio padrão de todos os desvios que mais nos interessa. Na figura
abaixo de uma falsa EV o desvio padrão de todos os desvios também é de 0,2
anos, embora se verifique claramente uma transição de baixa variabilidade para
elevada variabilidade.
A fim de poder
detectar diversos regimes de variabilidade, podemos fazer o seguinte: calcular
os sucessivos valores do desvio padrão num certo número de anos, por exemplo 6 anos
([12]). A primeira figura acima mostra, a traço azul, o resultado obtido para
os desvios da EV. O valor para 1979 é o desvio padrão para os anos de 1975 a
1979; para 1980 é o desvio padrão para os anos de 1976 a 1980; e assim sucessivamente,
até ao conjunto dos últimos seis anos. O gráfico não evidencia uma transição
entre diferentes regimes de variabilidade; o desvio padrão varia, com pequenas
excursões, em torno de cerca de 0,12 anos (escala vertical da direita). Para
efeitos práticos podemos considerar que o valor do desvio padrão é independente
do tempo.
Variáveis que
evoluem no tempo mantendo sempre a mesma média e o mesmo desvio padrão dizem-se
estacionárias. (Esta definição é suficiente para os nossos propósitos;
ver [13].)
Conseguimos
jogar sempre bem o jogo forward com a EV (ver artigo anterior: http://revolucaoedemocracia.blogspot.pt/2014/01/o-sector-financeiro-vi-jogos-com.html)
porque se tratava de uma evolução praticamente estacionária (depois de remover
a evolução linear). Não conseguimos jogar bem o jogo forward com a
cotação JPY/USD (ver gráfico no artigo anterior) porque a respectiva evolução
temporal não é estacionária. Claramente a curva JPY/USD não é rectificável por
transformação simples. O desvio padrão dos valores diários da cotação durante
um mês varia conforme mostra a figura abaixo (traço preto); a curva de
tendência a azul revela dois regimes de alta variabilidade até meados de 1991,
seguidos de um regime de baixa variabilidade. Em finanças usa-se muito a
chamada «volatilidade» como medida de variabilidade; trata-se do desvio padrão
dos incrementos relativos de uma dada variável (ver [14]); o gráfico da
volatilidade é parecido com o gráfico abaixo e as conclusões são as mesmas.
Seguros e
Derivados
Existem muitos
exemplos de variáveis quase estacionárias. Eis dois deles:
Evoluções
(séries) temporais tais como taxas de mortalidade por morte natural ou por
acidentes, prejuízos causados por incêndios, por furtos, por inundações, e, de
uma forma geral, todas as séries de eventos que caem na alçada das Companhias
de Seguros, são quase estacionárias a menos de uma dada transformação simples
(remoção de uma tendência linear em (a) e de uma tendência exponencial em (b)).
As Companhias de Seguros podem, com bastante segurança, jogar o jogo forward: prever montantes expectáveis de
indemnizações e, assim, os preços dos seguros.
Vejamos,
agora, alguns exemplos de séries não estacionárias:
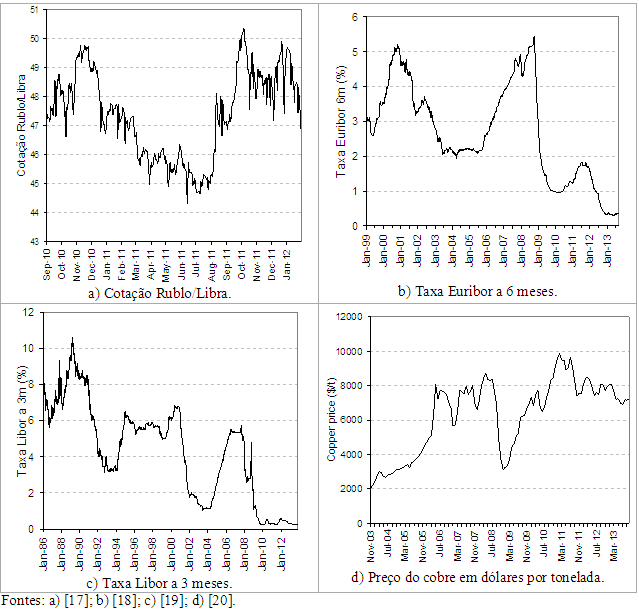
Taxas de juro,
cotações cambiais, cotações de valores mobiliários (acções, títulos de dívida,
etc.) e preços de matérias-primas como metais e petróleo, caracterizam-se por
evoluções não estacionárias. Nos exemplos acima vê-se claramente que não existe
um regime constante de média e variabilidade. Para além disso, não é possível
aplicar transformações simples que confiram estacionaridade às séries
transformadas.
Fazer
previsões com tais tipos de variáveis é sempre um jogo arriscado. Nenhuma
Companhia de Seguros joga este tipo de jogos; bom, até certo ponto... Estamos
no domínio dos jogos com derivados. No domínio da especulação financeira.
Na realidade,
existe toda uma larga teoria matemática que alguns entendem como conferindo
alguma «respeitabilidade» e «segurança» aos jogos com derivados. No próximo
artigo discutiremos este tema.
Uma
opção é um contrato que confere a um contratante – dito o detentor (ou comprador) da opção -- o direito (mas não a obrigação)
de comprar (no caso da opção de compra, call option) ou de vender (no
caso da opção de venda, put option) ao outro contratante -- dito subscritor
(ou vendedor) -- uma quantidade especificada de um activo, a determinado preço,
num data futura (opção europeia). Para usufruir do direito conferido pela opção
o detentor paga ao subscritor um prémio no momento do contrato.
Exemplo: A companhia inglesa XY vai ter de
efectuar um vultuoso pagamento em dólares. Aparentemente para se proteger de
uma apreciação do dólar, XY entra numa opção de compra a 90 dias com o banco UV,
pela qual paga a UV um prémio de 500 mil dólares com a possibilidade (mas não a
obrigação) de poder exercer a opção no montante de 10 milhões de dólares (10 M$)
ao câmbio de 1,6$ = 1£ (1,6$/£).
O câmbio acordado é o chamado preço de exercício, preço da libra
estipulado para o termo do contrato. O prémio corresponde a uma avaliação da
opção -- preço da opção. Suponhamos
que o contrato estipulava 0,05$/£. Com vista a usufruir do direito de comprar
os 10 M$ o detentor paga ao subscritor, na data de assinatura do contrato, 0,05x10
M$ = 500 mil dólares, 0,5 M$ (não entrando com o juro dos 90 dias, para
simplificar).
Suponhamos que 90 dias depois a libra vale 1,7$/£.
Como este valor é superior ao preço de exercício, XY exerce o contrato: obtém 10
M$ tendo ganho com a opção 10x(1,7-1,6) – 0,5 = 0,5 M$. UV perdeu a mesma quantidade. Se a libra
valesse 1,5$ XY não exerceria a opção, gastando apenas o prémio de 0,5 M$, que
UV ganharia. XY livrava-se, assim, de ter de pagar mais 10x(1,6-1,5) = 1 M$.
Note-se que uma opção -- como aliás todos os
derivados -- é também uma aposta sobre o futuro. Sobre o futuro de algo não
estacionário, logo largamente imprevisível!
* * *
Em 17 de Março de 1991 a Allied-Lyons anunciou
o espantoso prejuízo de 269 M$, cerca de 20% dos lucros projectados para 1991.
A Allied-Lyons era um grande conglomerado britânico do sector alimentar que se
meteu na especulação no mercado forex. Para tal, constituiu um departamento
financeiro específico encabeçado por um especialista com anos de experiência no
Crédit Suisse. Obteve retornos consideráveis comprando forwards em dólares.
Em Setembro de 1989, dada a elevada
volatilidade do preço do dólar, o departamento financeiro da Allied-Lyons
iniciou a subscrição de opções de
compra em libras. Por exemplo, em 1/6/1989 a Allied-Lyons subscreveu uma opção
de compra a 90 dias de um montante de 10 M$ pelo preço de exercício de 1,57$/£
e um preço de opção de 0,05$. Vejamos o que isto significa. Como subscritor, a
Allied-Lyons recebe logo de início o prémio de p = 10x0,05x(1+0,06/4) = 507.500$, onde no
prémio incluímos já a valorização do dólar à taxa de juro de 6% por um período
de 90 dias (para simplificar as contas tomámos ¼ do ano). Suponhamos que
passados 90 dias a cotação nesse momento é de 1,5$/£. Então, ao detentor da
opção não interessa exercê-la (a cotação do dólar em libras está mais baixa do
que o contratado na opção; mais vale comprar dólares no mercado cambial
normal). Logo, a Allied-Lyons fica a ganhar o prémio; e era com isto que a
Allied-Lyons especulava: apreciação do dólar face à libra implicaria embolsar
prémios. Mas, suponhamos, que a cotação ao fim de 90 dias é de 1,67$/£. Então,
o detentor exerce a opção e o subscritor, Allied-Lyons, tem de pagar os 10 M$
perdendo com isso (face ao câmbio do momento) 10x(1,67-1,57) = 1M$. Descontando
o prémio a Allied-Lyons perde 1 – 0,5075 M$ = 492.500 $. Mas o pior de tudo
deste jogo especulativo da Allied-Lyons é que as respectivas perdas podem ser
(em princípio) arbitrariamente elevadas! (Ver [21] para mais detalhes.) O jogo
da Allied-Lyons era um jogo especulativo de altíssimo risco. Na realidade, as
opções da Allied-Lyons eram algo mais complexas devido a cláusulas extra que
acabaram por penalizar ainda mais a Allied-Lyons.
-------------------------
Próximo
artigo:
Respeitabilidade e segurança?
Opções e o passeio aleatório
Opções e a fórmula de Black-Scholes
-----------------------------
Notas
[11] O desvio padrão para os seis primeiros desvios (ver tabela do
artigo anterior) é calculado assim: 1) os desvios de EV para a recta 15,1+0,137x(ano-1974)
são -0,444, -0,382, -0,019, -0.257, 0,106, 0,168, com média -0,138; 2) A soma
dos quadrados das diferenças para a média é (-0,444+0,138)2+…=
0,334; 3) o desvio padrão é a raiz quadrada de 0,334/6 = 0,236 (de facto devia
dividir-se pelo número de valores menos um, isto é, por 5 e não por 6; a razão
e a relevância disto são, aqui, sem qualquer importância). O valor 0,236 é o
primeiro valor da curva a azul.
[12] A chamada
«janela temporal» usada no cálculo do desvio padrão em sucessivos instantes de
tempo deverá ter uma «largura» temporal adequada. A discussão deste aspecto não
é aqui importante.
[13] A
estacionaridade é definida para processos estocásticos: distribuições
probabilísticas de um número arbitrário de observações de séries temporais.
Estamos aqui a considerar apenas a estacionaridade estatística, avaliada
numa janela temporal que percorre uma
única observação de uma série temporal, tal como acontece com as séries
económicas. Além disso, estamos a limitar-nos à chamada estacionaridade
restrita, apenas da média e do desvio padrão (ou de medida alternativa
associada ao momento corrente de segunda ordem da série temporal).
[14] A volatilidade num dado período de tempo é definida em finanças como o
desvio padrão dos incrementos relativos de uma variável económica nesse
período: stdev((Vi+1
– Vi)/Vi), onde Vi
e Vi+1 são
valores consecutivos da série temporal (respectivamente, no instante de tempo i e no instante seguinte, i+1) e stdev representa o desvio padrão.
Quando se trata de valores sempre próximos de Vi e Vi+1,
como é frequente em séries diárias, também se obtém praticamente o mesmo valor
da volatilidade usando stdev(ln(Vi+1/Vi)), onde ln
designa o logaritmo neperiano. De facto, se Vi+1
>= Vi, temos que Vi+1/Vi = 1 + a, com a pequeno (muito
inferior a 1); do mesmo modo, se Vi+1
< Vi, temos que Vi+1/Vi = 1 - a, com a pequeno. No
primeiro caso, ln(Vi+1/Vi) = ln(1+ a), que por desenvolvimento em série de
McLaurin se pode escrever: ln(Vi+1/Vi) = ln(1+ a) = a
– a2/2 + a3/3 - …≈ a, para a pequeno. De forma semelhante, ln(Vi+1/Vi)
= ln(1- a) = -a – a2/2 - a3/3 - …≈ -a. Ora, a no primeiro caso e –a
no segundo caso são simplesmente os incrementos relativos: (Vi+1 – Vi)/Vi.
Seja s a volatilidade num longo período de
tempo, de forma a poder considerar-se a volatilidade intrínseca da série, e
seja sT a volatilidade num
período limitado de tempo, T. Então,
o modelo do passeio aleatório determina que sT
= sxsqrt(T),
onde sqrt designa a raiz quadrada. Por aqui se vê que o passeio aleatório é não
estacionário (sT varia com
T). Num próximo artigo veremos também
que esse modelo, tão caro aos que trabalham na área de apreçamento de valores
mobiliários, é um modelo largamente inaplicável.
[15] Reported 1 or 2-Family Home Structure Fires: http://www.nfpa.org/~/media/Files/Research/NFPA%20reports/Occupancies/oshomes.pdf
[16] Traffic
Fatalities based on historical nhtsa and fhwa data http://www.saferoads.org/federal/2004/TrafficFatalities1899-2003.pdf
[17]https://www.google.com/search?q=oanda&sourceid=ie7&rls=com.microsoft:pt-PT:IE-Address&ie=&oe=;
http://fxtop.com/en/historical-exchange-rates.php
[20] World
Bank (Index Mundi); http://www.infomine.com/investment/metal-prices/copper/all/
[21] A posição do subscritor de uma opção de compra, como no caso da Allied
Lyons, é mostrada no gráfico abaixo. O gráfico da posição do detentor é
simétrico em torno do eixo horizontal.
Quando o preço no termo do contrato (S) é inferior ou igual ao preço de
exercício, E = 1,57$, o subscritor
ganha o prémio correspondente a 0,05x(1+0,06/4) = 0,5075 (que o detentor
perde). Quando S > E o ganho do subscritor diminui e
torna-se uma perda logo que S >
1,57+p =1,62 $ (aproximadamente). Com
S crescente as perdas são
arbitrariamente grandes. A posição de subscritor de opções (quer de compra quer
de venda) é sempre uma posição claramente
especulativa (mais detalhes em [9]).